Исследование эпидемиологических моделей распространения в сетях. Актуальность и новизна курсовых, дипломных и магистерских работ по эпидемиологическим моделям распространения, узнать рекомендации эксперта и скачать пример.
Модель SI
Рассмотрим классическую модель распространения фейков, которая делит всех пользователей на две группы. Модель SI представлена на рисунке 2.1. Все пользователи подразделяются на две группы: восприимчивые (S) и зараженные (I). Модель SI предполагает однонаправленное движение. После инфицирования зараженный пользователь уже не может вернуться в восприимчивое состояние.
| Состояние |
Определение |
| Восприимчивые S(t) |
Пользователи, которые не знают о фейке |
| Инфицированные I(t) |
Пользователи, которые знают фейк и активно распространяют его своим соседям |
Обозначения S(t) и I(t) представляют собой число восприимчивых и число инфицированных пользователей соответственно, в данный момент времени t. Общая численность пользователей составляет:
N=S(t)+I(t).
Каждый пользователь должен принадлежать одной из двух групп. При взаимодействии восприимчивых и инфицированных пользователей существует вероятность распространения фейка β. Это отражает выражение βSI, где β - вероятность передачи фейка от инфицированного пользователя к восприимчивому, SI – количество взаимодействий между восприимчивыми и инфицированными пользователями. Например, если β=0.7, то это означает, что фейк распространится в семи из десяти взаимодействий. Чем больше β, тем большее количество восприимчивых пользователей будет переходить в инфицированное состояние. Выражение βSI обозначает число пользователей, которые переходят в инфицированное состояние из восприимчивого. Выражение -βSI обозначает число восприимчивых пользователей, которые услышали фейк, и таким образом покидают восприимчивое состояние.
| Параметр |
Определение |
| β |
Вероятность распространения фейка от инфицированного пользователя к восприимчивому, 0<β≤1 |
Рассмотрим, как происходит распространение фейка по модели SI в зависимости от времени. Определим изменение количества восприимчивых пользователей. Пусть в момент времени t = 0 имеется один зараженный пользователь, а все остальные находятся в восприимчивом состоянии. То есть t = 0, I (0) = 1 и S (0) = N – 1. Таким образом
∆S=∆(N-1)=-∆I=-βI(N-I)∆t=(-βI(S+I-I))∆t=(-βIS)∆t.
Модель SIR
В модели SIR вводится еще одно состояние, к которому относятся восстановленные пользователи.
| Состояние |
Определение |
| Восстановленные R(t) |
Пользователи, которые знают фейк, распространяли его ранее, но больше не распространяют |
Общая численность пользователей определяется соотношением:
N=S+I+R.
Добавление состояния R не изменяет уравнение∆S, но изменяет уравнение ∆I следующим образом:
∆I=∆(N-S-R)=0-∆S-∆R=(βI(N-I)-rI)∆t=
=(βI(S+I-I)-rI)∆t=(βSI-rI)∆t,
| Параметр |
Определение |
| β |
Вероятность распространения фейка от инфицированного пользователя к восприимчивому, 0<β≤1 |
| r |
Вероятность перехода пользователя из инфицированного состояния в восстановленное, 0 |
Чтобы определить вероятность распространения инфекции в модели SIR, рассмотрим:
∆I=(βIS-rI)∆t.
Если выражение (βS-r) положительно, то количество заражений будет увеличиваться, когда S>r/β=P. P представляет собой относительную вероятность удаления которая определяет, когда произойдет эпидемия. Если выражение (βS-r) отрицательно, то количество заражений будет уменьшаться. Следовательно, при S
Если эти условия будут выполняться, распространение фейка не достигнет эпидемии. Для возникновения эпидемии в сети должно быть минимальное количество восприимчивых пользователей. Если количество восприимчивых пользователей недостаточно велико, то распространение фейка в конечном итоге затухнет. Но если количество восприимчивых пользователей велико и относительная вероятность удаления мала, то, скорее всего, эпидемия произойдет.
Определим, изменение числа восстановленных пользователей как ∆R. Предположим, что в момент времени t=0, I(0)=1, S(0)=N-1, то можем составить уравнение:
∆R=∆(N-S-I)=0-∆S-∆I=(0-0+rI)∆t=(rI)∆t.
Модель SIR имеет свои недостатки. Пользователи, активно распространяющие фейк, могут перейти в восстановленное состояние, но не имеют возможности перейти из восстановленного состояния в восприимчивое. В действительности же, люди часто вновь верят ранее забытой фейковой информации после того, как услышат новые сведения о фейке. Это может привести к тому, что пользователь станет восприимчивым к фейку. Этот недостаток исправлен в модели SIRS.
Модель SIRS
В модели SIRS вводится состояние, которое позволяет восстановленному пользователю перейти в восприимчивое состояние.
| Параметр |
Определение |
| β |
Вероятность распространения фейка от инфицированного пользователя к восприимчивому, 0<β≤1 |
| r |
Вероятность перехода пользователя из инфицированного состояния в восстановленное, 0 |
| γ |
Вероятность перехода пользователя из восстановленного состояния в восприимчивое, 0<γ≤1 |
Модель SIRS также имеет свои недостатки. Хотя она позволяет пользователям переходить из восстановленного состояния в восприимчивое, она не позволяет пользователям напрямую переходить из восстановленного состояния в инфицированное. Распространение фейков в реальной жизни многогранно, и нередки случаи, когда некоторые пользователи, забывшие фейк, могут узнать информацию, которая заставляет их снова поверить в фейк. Необходимо добавить большее количество состояний для более точного описания моделей распространения фейков и их последующего прогнозирования.
Модель SEIR
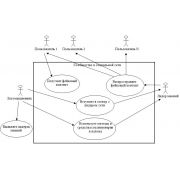
Рассмотрим модель SEIR в контексте распространения фейков. Данная модель представлена на рисунке 1.
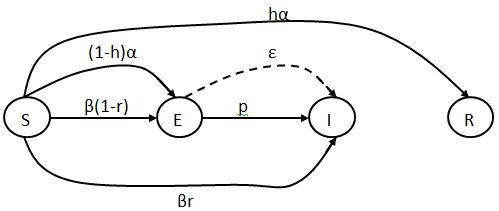
Рисунок 1 - Переход состояний в модели SEIR
| Состояние |
Определение |
| Латентные E(t) |
К данной группе относятся пользователи, которые знают фейк, но еще сомневаются в его истинности и не распространяют его |
| Параметр |
Определение |
| β |
Вероятность перехода от восприимчивого пользователя к зараженному или латентному, 0<β≤1 |
| β (1-r) |
Вероятность перехода пользователя из восприимчивого состояния в латентное, 0<β,r≤1 |
| βr |
Вероятность перехода пользователя из восприимчивого состояния в инфицированное, 0<β,r≤1 |
| p |
Вероятность перехода пользователя из латентного состояния в инфицированное через EI взаимодействие, 0 |
| ε |
Вероятность перехода пользователя из латентного состояния в инфицированное без взаимодействий, 0<ε≤1 |
| α |
Вероятность перехода пользователя из восприимчивого состояния в латентное или восстановленное, 0<α≤1 |
| (1-h) α |
Вероятность перехода пользователя из восприимчивого состояния в латентное, 0 |
| h α |
Вероятность перехода пользователя из восприимчивого состояния в восстановленное, 0 |
Модель SEIR состоит из четырех групп пользователей: восприимчивые (S), латентные (E), инфицированные (I), восстановленные (R). Число пользователей, которые покидают восприимчивое состояние после взаимодействия с инфицированными равняется βSI. В результате SI взаимодействия восприимчивый пользователь перейдет в инфицированное состояние с вероятностью βr, либо перейдет в латентное состояние с вероятностью β(1-r). Количество пользователей, которые покидают восприимчивое состояние после взаимодействия с восстановленными равняется αSR. В результате SR взаимодействия восприимчивый пользователь станет латентным с вероятностью (1-h)α, либо станет восстановленным с вероятностью hα.
Отметим тот факт, что восстановленные пользователи определяются как пользователи, которые не распространяют фейк, но вполне вероятно, что они попытаются доказать другим пользователям недостоверность фейка, тем самым продолжив его распространение. После латентного состояния пользователи могут перейти только в инфицированное состояние. Если латентный пользователь взаимодействует с инфицированным, то он перейдет в инфицированное состояние с вероятностью p. Латентные пользователи также могут переходить в инфицированное состояние без взаимодействия с другими пользователями с вероятностью ε. Если пользователь переходит в инфицированное состояние, то он уже не может его покинуть.
Модель SEIR тоже имеет свои недостатки. Один из недостатков состоит в том, что она не учитывает возможность пользователя покинуть инфицированное состояние. Другой недостаток заключается в том, что восстановленный пользователь не может стать восприимчивым или инфицированным. Также латентное состояние подразумевает, что пользователь еще не решил верить в фейк или нет, но пользователи могут переходить только в инфицированное состояние. Для большего соответствия действительности необходимо наличие перехода между латентным и восстановленным состоянием. Таким образом, введем модель SIHR распространения фейков.
Модель SIHR
Модель SIHR представлена на рисунке 2.

Рисунок 2 - Переход состояний в модели SIHR
Модель SIHR включает в себя состояния: восприимчивые (S), инфицированные (I), состояние гибернации (H), восстановленные (R).
Состояние гибернации (H) - пользователи, которые прочитали фейковую новость, но временно его забыли в силу того, что им не интересна данная тематика. Они могут вспомнить фейк в любой момент времени, и в конечном счете станут инфицированными. Они могут вспомнить фейковую новость самопроизвольно, либо же в результате взаимодействия с инфицированным пользователем.
Для модели SIHR существуют ограничения. Одно из ограничений заключается в том, что она не содержит группы пользователей, которые были восстановлены. Таким образом, она не позволяет некоторым пользователям решать, верить ли в фейковую новость или нет. Другим ограничением является то, что модель не позволяет восстановленным пользователям покинуть восстановленное состояние. Аналогичное ограничение было отмечено в модели SIR и SEIR.
Сравнительный анализ эпидемических моделей диффузии информации представлен ниже.
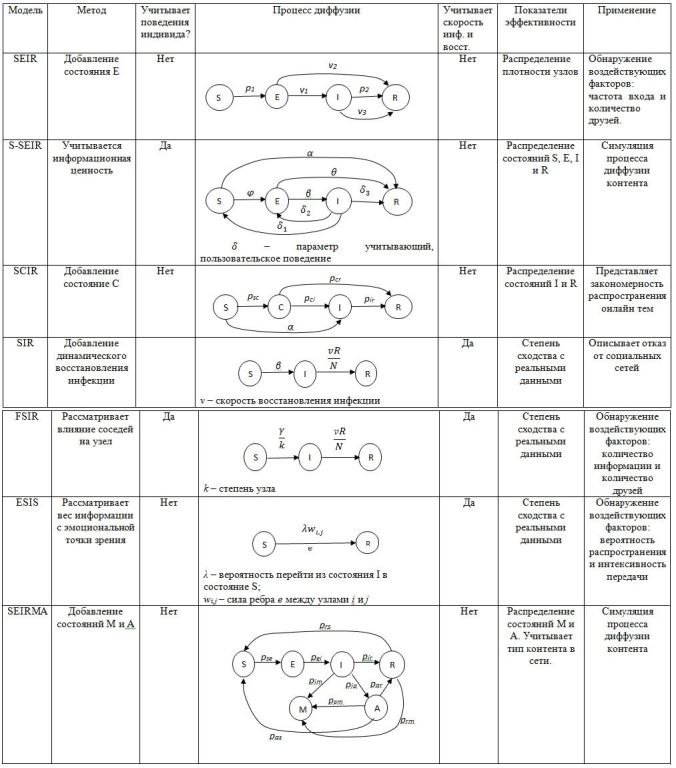
Таким образом, в данной статье были рассмотрены эпидемиологические модели, применяемые в исследовании социальных сетей.