Как написать дипломную работу на тему дискретного моделирования. Актуальность цели и задач во введении диплома, направления исследования, суть и особенности написания, а также готовый образец плана, содержания и заключения дипломной работы по дискретному моделированию. Узнать рекомендации экспертов и скачать пример дипломной работы бесплатно.
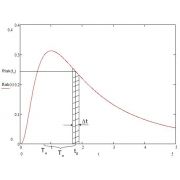
Дипломы по дискретному моделированию посвящены исследованию моделей, изменяющихся непрерывно во времени. Это модели движения в реальных координатах, модели химического производства и т.п. На рисунке 1 представлена дискретная модель.
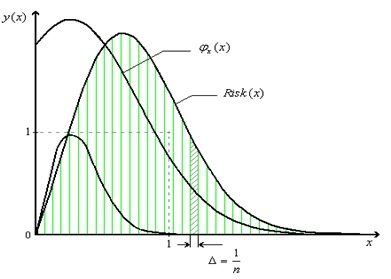
Рисунок 1 - Пример дискретного моделирования в дипломной работе
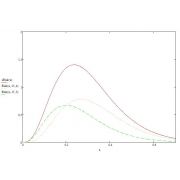
Несмотря на то, что дискретные модели являются абстракцией, существует широкая области применения таких моделей (подробно о разработке математических моделей изложено здесь). Так, например, при построении модели почтового сервера для оценки средней длины очереди запросов на прием-передачу писем пользователей и известных характеристиках обслуживания сервером сообщений можно абстрагироваться от этих второстепенных явлений и считать систему дискретной. В качестве примера можно привести рисунок 2, на котором представлена модель процесса при помощи сети Петри-Маркова.
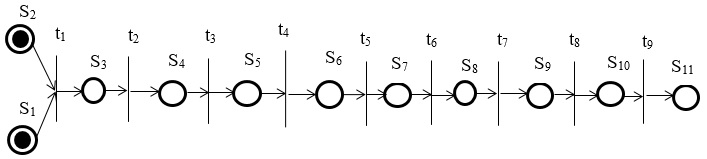
Рисунок 2 - Применение сети Петри-Маркова в дипломе по дискретному моделированию
В ряде случаев дипломы по дискретному моделированию посвящены исследованию непрерывных моделей, что характерно для системной динамики. Так, например, потоки данных в канале связи или пользовательская активность могут быть описаны в виде непрерывных переменных, описывающих интенсивности изменений.
В качестве примера дипломной работы по дискретному моделированию приведем этап выпускной работы по разработке микро фрактала дискретной модели заражения сети.
Особым вопросом следует считать построение фракталов вирусования в однородной среде отдельного слоя. Реальный теоретический и практический интерес представляет построение обобщенного фрактала, моделирующего процесс вирусования на микроуровне. Назовем его микро-фрактал, а звезду распространения эпидемии будем считать макро-фракталом процесса.
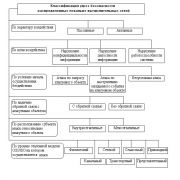
Обобщенно этот фрактал будет состоять из нескольких секций одного слоя (рисунок 3), верхние из которых относятся к процессу заражения, а нижние к процессу излечения.
.jpg)
Рисунок 3 - Обобщенная парадигматическая модель эффекта вирусной атаки вершин в однородном слое (микро-фрактал)
Между секциями имеют место быть вероятностные процессы, переводящие вершины (по дискретным их состояниям) из одного множества в другое:
S_s - множество здоровых в s - слое, но подверженных заражению вершин сети.
E_s - множество инфицированных вершин s - слоя, неспособных распространять инфекцию(инкубационные).
I_s - множество инфицированных вершин s - слоя.
D_s - множество выявленных в s - слое инфицированных вершин.
R_s - множество утраченных вершин s - слоя, потерявших работоспособность в результате заражения.
M_s - множество инфицированных вершин заранее, в результате излечения E_s и I_s.
Очевидно Е - секция выступает инкубатором инфекции, а D - секция - госпиталем для излечения от неё. Циклы обоих процессов должны вписываться в рамки времени дискретизационной модели, т.е. и инкубационный период, и длительность излечения, должны быть меньше этой дискреты.
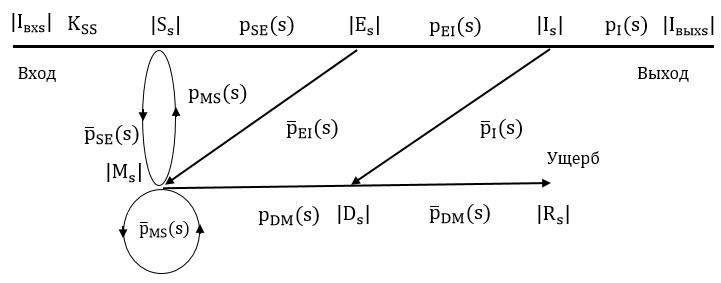
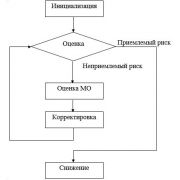
Рисунок 4 - Линейный граф микро-фрактала
Интересно отметить, что переход (SM) двусторонний, т.е. подверженные вирусованию вершины могут быть заранее на входе процесса частично переведены в множество иммунизированных вершин, ровно, как и иммунизированные вершины со временем, утрачивая свой иммунитет, могут становиться подверженными инфицированию. Кстати говоря, это возможно и при мутации вируса, когда он приобретает новое качество за рамками иммунитета, приобретённого вершинами. Здесь нужна перестройка работы D - госпиталя по стратегии излечения.
Данный микро - фрактал (рисунок 4) назван обобщенной парадигматической моделью ввиду того, что из этой структуры исключением тех или иных ее элементов возможно получить все известные парадигматические модели. К примеру, пренебрегая инкубационными вершинами и напрямую заводя связь от S и I, а также, не рассчитывая на иммунизацию вершин (убираются соответствующие процессы), получаем относительно простую SIR - модель. С другой стороны, полагая, что со временем или с связи с подтверждением нового вируса иммунизированные вершины теряют свои свойства и переходят в S - подмножество, фактически можно получить модель MSEIR.
Поэтому, опираясь на предложенный фрактал, можно с применить любую известную парадигматическую модель в описании эпидемических процессов. Задача фактически состоит лишь в том, чтобы определить для них вероятность p_s. Причем, разговор идет о пакете поступаюших на вход вирусных воздействий и важно вероятностно определить на выходе количество вторичных источников инфекции.
В заключение стоит отметить, что предложенная дискретная модель может быть модернизирована для прочих парадигматических конструкций типа SIR, SIRS и т.п. Полный перечень актуальных статей и рекомендаций по угрозам и рискам информационной безопасности изложен здесь.